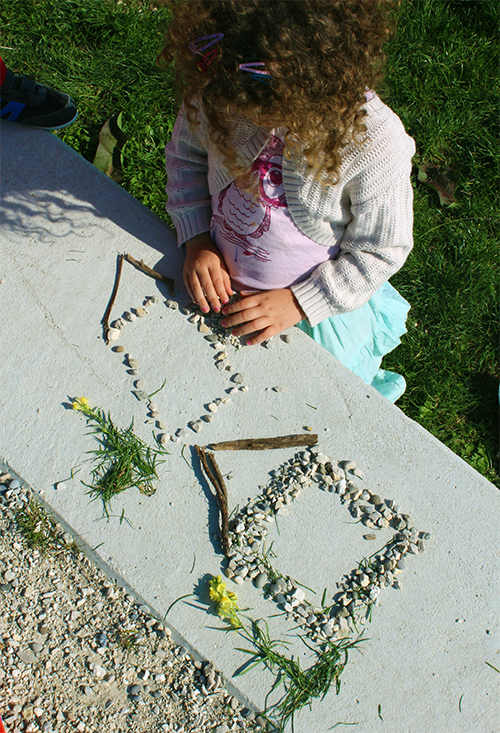Si vous vous êtes penchés sur la question des formes géométriques que l’on trouve dans la nature, vous aurez remarqué que certaines y sont de façon magnifique tel que le cercle, la spirale ou l’hexagone. Trouver des carrés ou des triangles en revanche, c’est plus compliqué ! Heureusement, la GeoBoard est là !
COMPÉTENCES :
(maths : géométrie)
– création, bricolage, mesure
– utilisation de la planche pour créer et comprendre certaines formes géométriques (carré, rectangle, triangle, triangle-rectangle…) et pour de nombreux jeux (à venir).

Pour fabriquer votre geoboard (planche de géométrie) vous aurez besoin d’une planche d’environ 40cm sur 30cm, d’une règle, d’un crayon et d’un paquet de clous. Nous avons décidé d’espacer nos clous d’un “pouce” (unité de mesure anglo-saxone), c’est à dire de 2,5cm. Au final ça n’a pas tellement d’importance, l’essentiel est que les espacements soient bien réguliers.
On trace à la règle les lignes verticales et horizontales et on place un clou dans les intersections afin d’avoir 15 clous horizontalement et 10 clous verticalement.


On cloue bien comme il faut…

C’est prêt ! Vous pouvez expérimenter, jouer, tester… En attendant on vous prépare des fiches d’activités sympa à faire avec cette planche 😀
L’autre avantage c’est qu’elle vous durera longtemps : on peut vraiment s’en servir à des âges très différents !